By oceanhead

Summary

We study a simple system, called the Baker’s Map, and we show that it exhibits all the characteristics of a chaotic system. Symbolic dynamics for the system will be constructed through the use of binary numbers. The system will be used as a model of a chaotic dynamical system for future articles.

No prerequisites are needed other than high school maths so all the additional mathematical tools and ideas used will be constructed throughout the article.

Sections:

1. Some Prerequisites
2. The Baker’s Map
   2.1) Presentation of the system
   2.2) Symbolic Dynamics for the Baker’s Map
   2.3) Metric compatibility and the dense orbit

1) Some Prerequisites

What we want to do in this short series of articles is to show the existence of a certain, very interesting behaviour in simple, abstract physical systems. This behaviour is called chaos, and is not an exceptional phenomenon: it is quite generic and we experience it in everyday life.

The context in which chaos fits best is called the theory of dynamical systems. This theory is at the crossroad between maths and physics, the discipline called mathematical physics. A dynamical system is the abstraction of a physical system. A dynamical system is essentially made of two parts, a set, called phase space or simply space, and a function, called the dynamics, that associates a point in the space to another point in the space. What we mean for space is already a complicated matter, and we won’t dive into it. For what we need, it suffices to think of the space $X$ as a subset of space, $X\subset {ℝ}^n$. The dynamics is just a function $\mathrm{\Phi }:X\to X$. This function is called dynamics because we want to think about it as a model of the motion of a particle: to do so, we think of a point $x$ in $X$ as a particle, and of $\mathrm{\Phi }(X)$ as the point in $X$ to which $x$ has moved to after a fixed time. The whole motion is calculated applying iteratively the dynamic map $\mathrm{\Phi }$ . For this reason, a rule that associates an “initial point” $x$ to its transform after $k$ units of time remains defined:

This means: chosen a time step $t_0$, the particle that was in $x_k$ at time $t=k{t}_0$, will be at time of $t=(k+1)t_0$ in position $x_{k+1}=\mathrm{\Phi }(x_k)$. This also means that if we want to know the position $x_k$ of a particle that starts its motion in $x_0$ after a time of $t=k{t}_0$, we need to apply $\mathrm{\Phi }$ to $x_{0}k$ times:

So this is the picture: we take a point $x\in X$ and we consider the subset

called orbit of $x$, and we think of the integer $k\in \mathbb{Z}$ as a time unit. What we want to do when analyzing a dynamical system is to describe qualitatively what the dynamical map does to the points in phase space $X$.

2) The Baker’s Map

2.1) Presentation of the system

We now concentrate on a single, simple dynamical system, called the Baker’s Map.

The phase space of the system is the square of unit length (with the edges removed), $X={[0,1]}^2$, which we will consider with Cartesian coordinates:

The dynamical map might seem a little complicated but with some figures it can be explained very easily. This is its form:

To visualize it, consider Figure 1. It is a plot of 50 000 random points in $X$, centered in $(\frac{1}{2},\frac{1}{2})$. Think of $X$ as a square of something malleable, like dough. The Baker’s map does what a baker does when working dough: you take the dough, you squash it down, you cut it in two and you put a piece on top of the other. If you are not convinced that this is what the map does, the figures will show you that this is exactly its action.

Think of the black ball as a dot of food coloring dabbed in the middle of the dough.

FIGURE 1: A ball of radius 0.1 of 50 000 random points in $X$

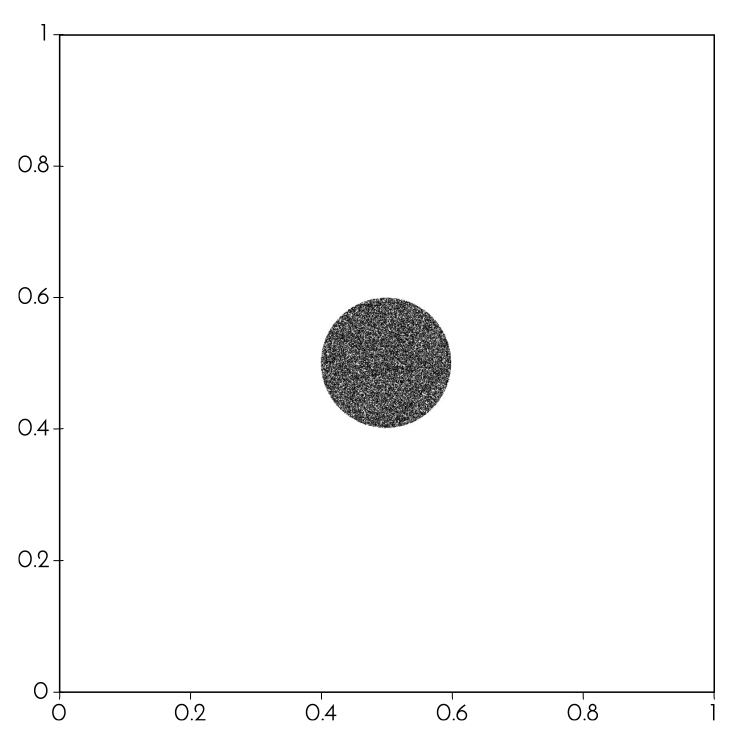
Note that the dot is exactly centered in the square. This has consequences on the speed with which the ball will be transformed, because the map is piecewise: that is, it does different things left of $x=\frac{1}{2}$ then it does right. In Figure 2 you can find a schematic drawing of the action of the map on the phase space. The iterations of the Baker’s map on the initial ball can be found in Figure 3. Think of the dough being squashed down until it’s twice as long and half as tall. Then it is cut in two, and the two parts are stacked. If you keep this in mind, the first iteration of the map will be clear to you: the ball is cut in two and half as tall. Now let’s take the resulting phase space and let’s apply the dynamics again, obtaining the second iteration. This time no part of the black dot has $x=\frac{1}{2}$, so the cutting has no effect on it. The result is that the black dot is only squashed, and it progressively gets longer and closer to the middle. This goes on for a while, until the two “limbs” are squashed and elongated enough that a piece of them intersect the half. We can jump to the fourth iteration, where a qualitative change ensues. This is when the magic starts! The limbs get repeatedly cut and stacked together, forming long and progressively finer filaments that, step by step, cover the whole phase space, making the points sparcer and sparcer. After 10 steps there is still a glimpse of regularity: we can still distinguish the filaments. This form goes on for some time, depending on the number of points that make the initial ball. The next steps make the points limbs lose their structure, distributing the particles throughout the dough. In this case, the phase space will go under another “transition” after 10 steps, in which the filaments are completely disintegrated.

The ball structure is completely lost. The points from now on wander around the dough, and no qualitative change ensues from now on. This is the situation of iteration 20.

It is clear that something “chaotic” is going on: after some steps, any “definite lump” in phase space will loose all its shape and will have its points distributed throughout the phase space (this is why bakers use¹ the baker’s map to kneed dough: all the lumps get distributed in the dough and after some steps the dough is almost perfectly uniform). What we want to show in the next section is that even if the system tends to rip up and uniform in phase space, it is deterministic.

2.2 Symbolic Dynamics for the Baker’s Map

Let’s focus on the action of the Baker’s map on one point. Can we predict where it will go after $k$ iterations? The first idea is to take its coordinates, apply the map, then plug the result in the map, and repeat $k$ times. This surely will show the point’s coordinates after $k$ iterations. But this is not an interesting way to do it, because we would like to predict without having to do all the calculations.

There is actually a way to predict the behaviour of one point’s orbit, more precisely, there is a way to find a point that will spawn an orbit that, iteration after iteration, will pass infinitesimally close to points we have chosen. To see this, we have to find smarter coordinates on phase space that are adapted to the map’s action, equivalently, coordinates in which the map’s action is extremely easy.

To do this, we must recognise what the map essentially does. As we have said, apart from the cutting, the map stretches in one direction and squashes in the other, and it does this by a factor of $2$. Stretching by a factor of $2$ is done by multiplying by $2$, while squashing is done by dividing by $2$. So the essential part of the map a division by two in one

FIGURE 2: Scheme of the Baker's map's action on a cat's paw. FIGURE 3: Iterations of the Dynamical Map.

direction, and a multiplication in the other. This gives us an idea: in base $2$, multiplying by $2$ is equivalent to adjoining a $0$ at the end of the number, equivalently, shifting towards the right the decimal point, while dividing by $2$ is equivalent to shifting towards the left the decimal point. Thus if we write the coordinates in $X$ in binary notation we can capture the stretching/squashing propriety of the map easily. This is actually an intermediate step, because we need to take account of the “cutting in two” part of the map. A deeper analysis of the map shows that the best coordinates² possible are these: you take the binary expansion of the point $(x,y)$

Note that these expansions are not necessarily finite, and if they are we will think of them as infinite by adjoining an infinite sequence of zeroes, in this way:

Then³ you take the binary expansion of $y$, reverse it and “attach” it to the binary expansion of $x$, this way:

So now, instead of phase space $X$ and it's points we will consider the set

of double-infinite “strings”, or “words”, with “symbols”, or “letters”, in $\{1,0\}$. The correspondence is one on one, because all we done is to find a compact way to write a point in $X$, and it is actually a function

For example, let’s consider the string associated to the point $(\frac{1}{2},0)$. The binary expansion of $\frac{1}{2}$ is $0.1$, so $h(\frac{1}{2},0)=\mathrm{\dots }00.10\mathrm{\dots }$

Now we need to find a map $\mathrm{\Psi }:\mathrm{\Sigma }\to \mathrm{\Sigma }$ that does what Baker’s map does on $X$.

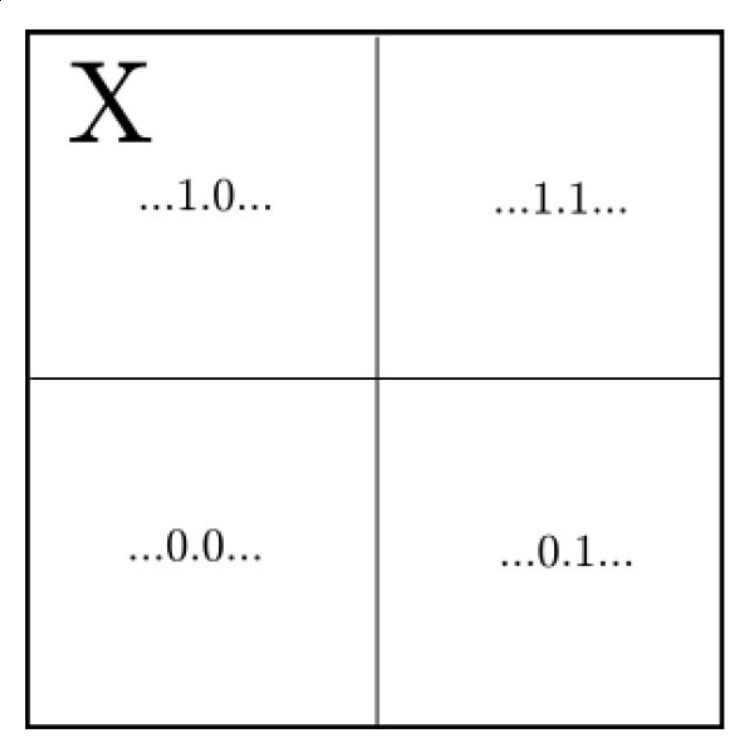
To do this we must understand what the binary expansion tells us about the points in phase space. Let’s focus on the $x$ component. Any $x$ such that will have binary expansion starting with $0$, that is $x=0.0\mathrm{\dots }$, while any $x$ such that will have binary expansion starting with $1$, $x=0.1\mathrm{\dots }$. This means that any point right of the center $(\frac{1}{2},\frac{1}{2})$ will be of the form $\mathrm{\dots }{\sigma }_{-1}.0{\sigma }_1\mathrm{\dots }$ and any point left of the center will be of the form $\mathrm{\dots }{\sigma }_{-1}.1{\sigma }_1\mathrm{\dots }$. The same thing can be said about the $y$ component, switching right with under and left with over. This means that if we divide in four quadrants our $X$, the letters in position $-1$ and $0$, tell us in which quadrant the point is. This reasoning can be repeated with the next two letters of the string, dividing each quadrant in additional four quadrants, and so on: the letters in position $k$ and $-(k+1)$ tell us in which square of a grid of $2^{2k}$ squares in $X$, the point is. See figure 4. This is essentially the meaning of a binary expansion, so it is nothing new but a different point of view. So a string localizes a point in $X$, with precision growing with the number of letters of each string we consider. This will be important for proving some fun properties peculiar to the Baker’s map.

Recall that the Baker’s map is defined by

We now prove that

FIGURE 4.1: Phase space partitions and letters in strings.

that is, on the word set $\mathrm{\Sigma }$

the Baker’s map acts as a translation towards the right of the decimal point:

FIGURE 4.2: Phase space partitions and letters in strings.

This is actually very easy to prove, in fact, we already proved it. To understand this let’s concentrate on the points with . Their associated strings in word space are the strings of the form $\sigma =\mathrm{\dots }{\sigma }_{-1}.0{\sigma }_1\mathrm{\dots }$. Since , the first part of the map applies, so $x$ is multiplied by $2$ and $y$ is $1$ divided by $2$. Notice that since after the division . On string space this means that ${\sigma }^{\prime }=\mathrm{\dots }0.{\sigma }_0^{\prime }$ The value of ${\sigma }_0^{\prime }$ depends on if or not: since ${\sigma }_0^{\prime }$ tells us in which sub-quadrant of the first 4 quadrant of $X$ the point is, and since the $x$-component of such point comes from a multiplication by two, if ${\sigma }_1$ was $0$ now ${\sigma }_0^{\prime }$ is $0$, and the $1$ same with $1$. To finish, note that if $x\ge \frac{1}{2}$, then $\mathrm{\Psi }$ brings the $1$. from $x$ to $2y$. Thus ${\sigma }^{\prime }=\mathrm{\dots }{\sigma }_0{\dot{\sigma }}_1{\sigma }_2\mathrm{\dots }$. A straight forward calculation may be needed to grasp this fact fully. You may try with the point $(\frac{1}{4},\frac{3}{4})$ and $(\frac{3}{4},\frac{7}{8})$

This result may be summarized by the concise formula⁴

These “coordinates” are called symbolic dynamics for the Baker’s map, because instead of looking at the evolution of the system in phase space, from now on we will look at the evolution of strings in word space. This may seem useless at first, but in this way we will prove important properties of the system. The first thing we will do is to use the symbolic dynamics to find points that spawn predetermined orbits. Consider this (weaker) problem: we want to find a point $P=(x,y)$ in phase space that after $k$ iterations of $\mathrm{\Psi }$ has $x>\frac{1}{2}$ (or $x\le \frac{1}{2}$). This is a very easy problem: since $\mathrm{\Psi }$ acts as translation of the decimal point on string space, every string $\sigma$ that has ${\sigma }_k=1$ (or $0$) will have its $k$-th iteration with the letter $1$ right before $1$ the decimal point, so it will certainly have $x>\frac{1}{2}$. Now, if we want to $1$ have $y>\frac{1}{2}$ too, then, for the same reasons, all strings with ${\sigma }_{k-1}={\sigma }_k=1$ will have their $k$-th iteration as wanted, because ${\mathrm{\Psi }}^k(\sigma )=\mathrm{\dots }1:1\mathrm{\dots }$. The points we are looking for are then simply $P=h^{-1}(\sigma )$. This reasoning can be further extended to any finer partition of $X$ in squares, in fact, if you find a string $\sigma$ with a block of $2s$ predetermined letters in it starting from position $k-s$, then after $k$ iterations of $\mathrm{\Psi }$ the string will have this block in center position, divided by the decimal point, thus the point $P=h^{-1}(\sigma )$. will be in the cell that is described by that block of letters.

The last generalization that can be made with the same reasoning is that instead of considering only a fixed number of iterations $k$, we could be interested in points whose orbits “hop” in given squares of some partition of $X$. This is now easy to construct: if the partition of $X$ has squares with sides of length $\frac{1}{2^s}$, all we have to do is to take a string that is in blocks of $2s$ letters that describe the wanted square, and let the $\mathrm{\Psi }$ map progress in steps of $s$. Every anti-image $P=h^{-1}(\sigma )$ at these fixed steps of $s$. iterations will clearly be where we wanted it to be, realizing our intent. So if we had fixed some points in phase space, then this point will have its orbit pass as close as we want to these points, just choosing a fine partition of phase space and letting the orbit go in squares that contain the fixed points. This tells us a second meaning of the strings: they describe the history of a given point.

There are two very important things to be noted: in the above construction, if the point $P=h^{-1}(\sigma )$ were to be taken with a small error, then after a few iterations the orbit would diverge from the one predetermined by $\sigma$ exponentially fast⁵. Somewhat similarly, if instead of a point we take a few points condensed in a small square of our fine partition, then they will be scattered throughout the whole phase space, in an uniform manner. These two considerations will motivate the definitions of a dynamical system and a chaotic dynamical system.

2.3 Metric compatibility and the dense orbit

What we want to analyze is the so-called metric structure of $X$. and $\mathrm{\Sigma }$. A metric structure is, very informally, a way to measure distances in a space. A little more formally, a metric on a set $Y$ is a function $d:Y\times Y\to [0,+\mathrm{\infty }]$ satisfying some more or less obvious requisites:

They mean: two points are distant $0$ if and only if they are the same point, distance does not depend on which point you compute it, and the third is called “triangle inequality” and essentially it means that the length of one side in a triangle is less than the sum of the length of the other two. The last requisite is there to restrict the possible metrics to the ones that are at least similar to the usual Euclidean metric defined by Pythagoras' theorem (see below). The couple is called metric space. $(Y,d)$ In $X$ there is an obvious metric: if $P$ and $Q$ are points, then we can define the distance between $P$ and $Q$ this way

which is just the Euclidean length of the segment joining $P$ and $Q$. There also is a metric on $\mathrm{\Sigma }$:

Since the sum is infinite, the $2^{-|k|}$ term is there to make it converge, that is, to have it return a finite number for every two strings in word space. Ignoring the subleties, it is easy to see that such metric is well defined and is a real metric. Its meaning is that two strings are closest when they have the same symbols in the same positions (and so they are the same string). The $2^{-|k|}$ term also guarantees that the strings that differ only on terms with large $k$, are still close.

Thinking about the meaning of the strings, you can see that this is a good thing.

So $(X,d_X)$ and $(\mathrm{\Sigma },d_{\mathrm{\Sigma }})$ are two metric paces: does the symbolic dynamic

send close points in close strings? In mathematical terms, we are asking:

The answer is no! As a matter of fact, the key is that we have eliminated from $\mathrm{\Sigma }$ all the strings that end (or begin) with an infinite succession of $1s$, and that lets us get as close as we want to a point that has no image in $\mathrm{\Sigma }$. But all is not lost, because it is true if we substitute $h$ with $h^{-1}$, and that is the “direction” we are interested in, since we want to prove things in string space and then transpose them in phase space. The last thing we prove about the Baker’s map is that there exists a point that spawns an orbit with a peculiar metric property:

That is, the orbit of $P$ passes as close as we want to every point of $X$. This is called a dense orbit. Another way of seeing this property is that if we draw point after point of the orbit of $P$ in $X$, we eventually⁶ fill the whole phase space without leaving any gaps.

As we have seen, the fruitful idea is to try to construct a string whose image under $h^{-1}$, and has the metric property we are looking for. To do this, note that given a generic string, if we truncate it left and right and we append zeroes to it, we obtain another string that is close to the beginning one, and we can decide how close such string is by deciding how many letters we truncate from the initial string. Then we note that we can order the set of such “finite” strings, for example in this way:

Then we consider the string that is composed by an arbitrary semistring on the left and on the right all the set of finite strings written one after the other, and the respective point in $X$:

We assert that this point’s orbit is our dense orbit. Indeed, choose $ϵ>0$ as small as you want, and let $k\in \mathbb{Z}$ be such that . For every

$Q\in X$, let $\tau =h(Q)$. The block ${\tau }_{-k}\mathrm{\dots }{\tau }_{k-1}$ is certainly somewhere in $\sigma$, since it contains all finite blocks of letters. Suppose it is in between positions $t-k$ and $t+k-1$ for some $t\in \mathbb{Z}$. Then after exactly $t$ iterations of the dynamical map the block will be centered around the decimal point in the iterate of $\sigma$, and at that moment the iterate will be less than $ϵ$ away from $Q$.

---

1. Actually, as far as I know, they use a different map, that in jargon is called Horseshoe map, in which the cutting is replaced by folding in half. Their behaviour is quite similar though, and they are both chaotic. ↩︎

2. To be precise, what we are considering is not a proper change of coordinates, since we are not changing the way we describe the phase space, but we should think of it as a dynamical conjugation, that is, we are looking for an equivalent dynamical system, in a certain sense. We will expand this point of view further in the next article, when we introduce the formal definition of a dynamical system. ↩︎

3. We should eliminate all the numbers with an infinite sequence of ones at the end, such that the change of coordinates is bijective. This means that if the expansion were decimal, we would not distinguish between $1$ and $0$.$\overline{9}$ which is a good thing. ↩︎

4. This is what we called dynamical conjugation earlier. ↩︎

5. The exponential character comes from the fact that every iteration multiplies $x$ by $2$ and divides $y$ by $2$. ↩︎

6. after an infinite amount of time ↩︎