by peeping_Tom

Cryptography is the practice of secret writing where information is hidden from adversaries. First used by the military, it is now used in every facet of our lives, from simple web browsing to paying bills, talking to your friends, and much more. With examples, I will show you the basics of cryptography and how all encryption is crackable. Cryptography is a wide topic that takes much mathematical ingenuity, so I sliced it into two parts. In this first part, we will explore the origins of cryptography and some simple ciphers you might use with your buddies online or off. This article is mostly theoretical but I encourage you to put your newly acquired knowledge to practice by coding working examples.

Encryption is based on the idea that cracking takes time, and that the more time it takes to crack, the better. Think of bike locks. We know they do not offer perfect security, but we rely on the idea that it will take bad people more time to break them than it will take for someone on the street to stop them. Cryptography follows a similar mindset.

The simplest cipher (method of encryption or decryption) is the substitution cipher. As its name implies, this cipher substitutes letters. The most famous substitution cipher is the Caesar cipher in which all the letters are replaced by their neighbors in the alphabet a few places over to the right or left. Imagine if A became B, B became C, C became D, and so on until we got to Z, which became A. This is a basic example of the Caesar cipher.

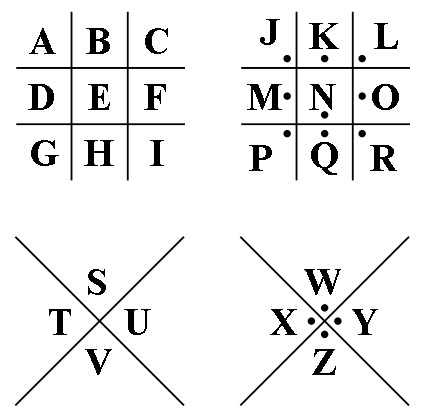
Another interesting substitution cipher is the Pigpen cipher. Used primarily by Freemasons, this cipher substitutes letters for shapes and dots.

Every substitution cipher works on the same simple idea, substitution of letters for some other symbols. The way anyone would go about cracking this cipher is through a “checking” process: look for common words in the message’s language, then substitute in reverse. For instance, you would look for repeated sets of 3 letters, expect them to be “the”, then carry out the necessary substitution on the rest of the ciphertext, i.e., the encrypted text.

Extend this process to letters, rather than for words, and you get something called “frequency analysis”. This method cracks any substitution cipher if you know the language of the plaintext (original message). To crack any substitution cipher you start with the “fingerprint” of the plaintext’s language, and then look at a frequency analysis of symbols in the ciphertext to see the rules for substitution.

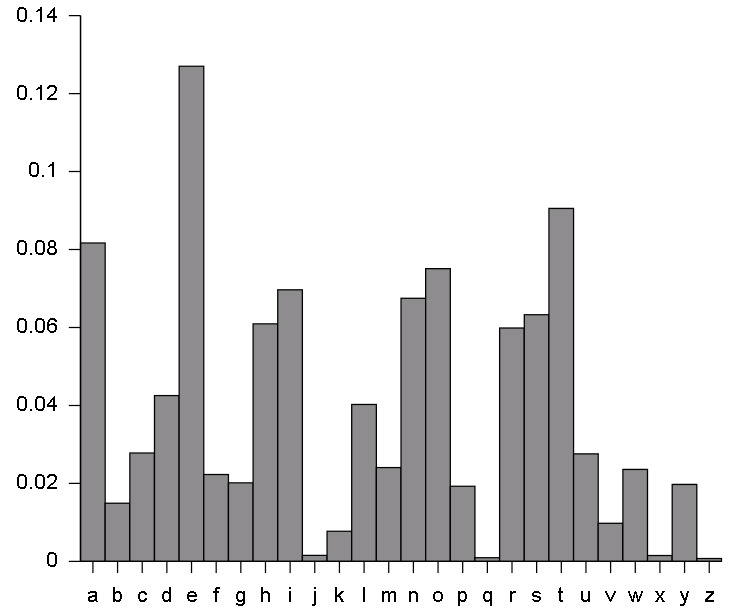
The fingerprint is simply a frequency of occurrence of some letters in a language. For example, if you were to take this wall of text and count the occurrences of every letter, you would find that the most common letters are (by total count): ‘e’, ’t', ‘a’, ‘o’, ‘i’, ‘n’, ’s', … (just remember ‘ETAOIN SHRDLU’ and that way you remembered the 12 most common English letters). The following image shows the fingerprint of the English language.

This property is unique to the English language, however all languages have a “common letter use” property. To evade this, people built the polyalphabetic cipher.

The polyalphabetic cipher works on the same idea as Caesar cipher, making multiple shift ciphers of the same plaintext. First, a codeword is established between the parties. The codeword denotes the shift ciphers, for example the codeword “snake” means that there are 5 shift ciphers each with their own designated shift. The first cipher substitutes the first ‘A’ to occur with ‘S’, ‘B’ with ‘T’, … the second ‘A’ with N', ‘B’ with ‘O’, and so on. Now that we have 5 shift ciphers with different letter shifts, how do we apply them to the plaintext? We repeat the ciphers in order. The first cipher on the first/sixth/eleventh/… letter, second cipher on the second/seventh/twelfth/seventeen/… letter, and so on. The most famous of polyalphabetic ciphers is the Vigenére cipher, which I have just explained.

Take the initial left column to be the codeword, and first row to be the plaintext or ciphertext you want to encrypt/decrypt. Repeat the codeword over the letters of the plaintext/ ciphertext without any spaces. For example, try to decrypt “WEBFCSLYZVMYCPN” with codeword “lainchan”. How would a cryptanalyst try to crack this? Since it’s just many Caesar ciphers, frequency analysis of the ciphertext is safe bet, right? Well, after he does that he is presented with flat or equally distributed letter frequency. That’s because there were several different shifts performed on one text. If he doesn’t know the codeword, he can’t really crack it. Unless he knows the length of codeword.

Since we know that the length of the codeword is N letters, and that every 1+K×N letter shares the same shift cipher (where K is a number from 0 to infinity – or at least until K×N becomes longer than ciphertext), we can do frequency analysis on every K×N-th letter. Since we used “lainchan” as our codeword, we can do frequency analysis on every 8th letter in “WEBFCSLYZVMYCPN” and find out all 8 shift ciphers that way, or in English, we can find the codeword. If we don’t know the length of the codeword, and we saw flat distribution of frequency analysis, then we would try frequency analysis of every (1+K×N)th letter, where K ranges from 0 to infinity. Since we don’t know N (length of the codeword), we will assume it’s 1 letter long, then we will assume its 2 letters long, and so on. We do this until we get the original, readable plaintext. This process can be automated with computers, which easily make it take less time. Longer codewords result in stronger ciphers since the cracker has to assume all possible codewords shorter than the real codeword.

This is only possible because the codeword is repeating, but what if it wasn’t repeating? What if we had a codeword as long as the plaintext itself? This is called a one-time pad. The codeword “lainzine” can be seen as a list of numbers by which the shift is occurring in each shift cipher (‘L’ = ‘11’, ‘A’ = ‘0’, ‘I’ = ‘8’, and so on). Also note that having a random number sequence for codeword is much more secure than having a word.

A multiple-shift cipher with random shifts on each letter that is as long as the ciphertext is unbreakable by frequency analysis because the shifts don’t repeat. The only way to break this one-time pad is brute force.

Bruteforce, in layman’s terms, is trying out every possible combination. Since we know that shift ciphers can shift letters by at most 26 until they repeat (as there are only 26 letters in the alphabet that you can shift to), bruteforcing a Caesar cipher would be simple since the shift is always the same. So you try out all possible shifts (from 1 to 26). For the polyalphabetic cipher and the one-time pad, bruteforcing becomes impossible since there is a shift for every letter. You would need to try all possible letter shifts for all possible letters, meaning that you would need try out all 26 shifts for only one letter. The longer the ciphertext is, the greater amount of shifts you need to try out. Given that’s 26 shifts for a letter, and N is the amount of letters in the ciphertext, you would need 26^N tries to crack the text. Best explained by a simple example.

Let’s say that we encrypted word “lainchan” with one-time pad with codeword of “ZDXWEJKA”, making it “KDFJGQKN”. There are 26 possible shifts for all letters, making it 26×26×26×26×26×26×26× = 268 = 208,827,064,576 possible combinations of shifts. As the plaintext becomes longer, N becomes larger and so does the amount of possible outcomes 26^N. If the codeword is truly random, one-time pads are on par with asymmetric encryption. If you have a friend with whom you can practice encryption, try remembering π to 300 decimals (it’s not that hard, just listen to Hard n' Phirm’s Pi song a bit and you already have 160 digits), and then encrypting everything with it (first letter shift by 3, second by 1, third by 4…).

Although the codeword needs to be truly random, this would work fine as long as you and your friend don’t reveal the codeword to anyone else.

That’s about all we need to know about the origins of cryptography and simple ciphers. In the next article, we will talk about XOR and asymmetric encryption. I hope you liked this short introduction, and that you will have loads of fun with your friends armed with this knowledge.